Guía Nº 1: Estática
En estos ejercicios veremos los diferentes sistemas de fuerzas en equilibrio



La esfera de 100 kgf de peso está suspendida de la cuerda A; de la cuerda B se tira como muestra la fig. de manera que la cuerda A forme un ángulo con la pared de 30º. Calcular la tensión que debe soportar cada soga.
R: TA=116 kgf ; TB=58 kgf
Ejercicio nº 3
Ejercicio nº 1
Los cables de la fig. forman con el techo un ángulo de 35º. Qué tensión soporta cada uno para equilibrar el peso de la lámpara de 59 kgf .
R: 51,7 kgf
Ejercicio nº 2
El cuerpo de la fig. pesa 50 kgf, calcular la tensión que debe soportar cada uno de los cables para mantenerlo en equilibrio.
R: 38,4kgf , 31,9kgf
Ejercicio nº 4
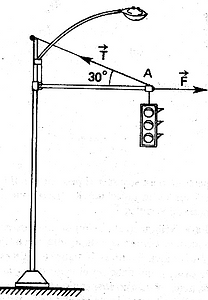
Un semáforo está sostenido como se indica en la fig.; el peso del mismo es de 20 kgf. La tensión del cable y la fuerza F que realiza el travesaño lo mantienen en equilibrio. Calcular dichas fuerzas.
R: T= 40 kgf ; F=35 kgf
Ejercicio nº 5
Un bote esta sujeto a las dos orillas de un canal mediante dos sogas, una forma con la orilla un ángulo de 33º y la otra uno de 60º. La corriente de agua arrastra al bote con una fuerza de 88 kgf; calcular la fuerza que debe soportar cada una de las sogas para lograr que la embarcación quede en equilibrio.
R: 48 kgf ; 76 kgf
Ejercicio nº 6

Calcular las tensiones de los cables en el esquema de la fig. para mantener en equilibrio el peso que se indica.
R: Tp=1800kgf ; Ts=2400 kgf
Ejercicio nº 7
Ejercicio nº 8
Ejercicio nº 9


La tensión del cable A es de 120 kgf, y el parante B soporta una fuerza de 70 kgf, manteniendo así el peso de la estrella en equilibrio. Calcular el peso de la misma.
R: 113,6 kgf
El cuerpo de la figura pesa 300 kgf , está suspendido del cable de una grúa en la forma que se indica . Calcular las tensiones del cable A y del parante B.
R: 113,6 kgf

Según los datos que se indican calcular la intensidad de F2 para que el sistema esté en equilibrio.
R:108,4 kgf
B) Momento de una fuerza – Equilibrio de palancas
Calcular la intensidad de la fuerza que se indica para que las siguientes palancas estén en equilibrio:




Repetir el problema anterior teniendo en cuenta ahora el peso de las palancas y suponiendo que las mismas son homogéneas. Peso palanca = 15 kgf.
R: 21,53 ; 117,5 ; 26,79 y 15,36 kgf
De la barra de la figura se cuelga una carga de 500 kgf a 2 m de la pared. Calcular la tensión del cable y la reacción horizontal (Rx) en la pared, sabiendo que la barra es homogénea y pesa 45 kgf.
R: T= 650,5 kgf ; Rx= 611,2 kgf

Ejercicio nº 1
Ejercicio nº 2
Ejercicio nº 3
Ejercicio nº 4
Repetir el problema anterior si ahora se coloca el cable a 3 m de la pared con el mismo ángulo. ( la palanca es la misma.
R: T= 1084,3 kgf ; Rx= 1018,9 kgf
Se cuelga un cartel de 150 kgf de peso con su centro de gravedad a 2,1 m de la pared, como se ve en la fig. El travesaño es homogéneo, pesa 30 kgf y tiene una longitud 2,5m. Calcular la tensión de la cuerda para mantener en equilibrio el sistema.(AB=2m)
R: 515,3 kgf
Ejercicio nº 5

Ejercicio nº 6
Repetir el problema anterior colocando el cable tensor en el extremo de la palanca. Qué ocurrió con el resultado, comparar con los problemas 3 y 4. Explicar.
R: 412.25 kgf.
Ejercicio nº 7
La palanca de la portada esta apoyada en su centro de gravedad, el elefante pesa 1500kgf y su centro de gravedad se ubico a 2m del apoyo; con una fuerza de 45kgf cuánto debería medir el otro lado de la palanca para lograr el equilibrio; por qué no nos interesa el pesa de la palanca.


